[GUEST ACCESS MODE: Data is scrambled or limited to provide examples. Make requests using your API key to unlock full data. Check https://lunarcrush.ai/auth for authentication information.]

![avalonaval Avatar](https://lunarcrush.com/gi/w:24/cr:twitter::1499498649310609415.png) ༀ Ω ChRθηθδ 𓂀 Merlin @ 𝔸𝕍𝔸𝕃𝕆ℕ ISLAND ☥ ⟲↯⟳ [@avalonaval](/creator/twitter/avalonaval) on x 1064 followers
Created: 2025-07-18 23:04:47 UTC

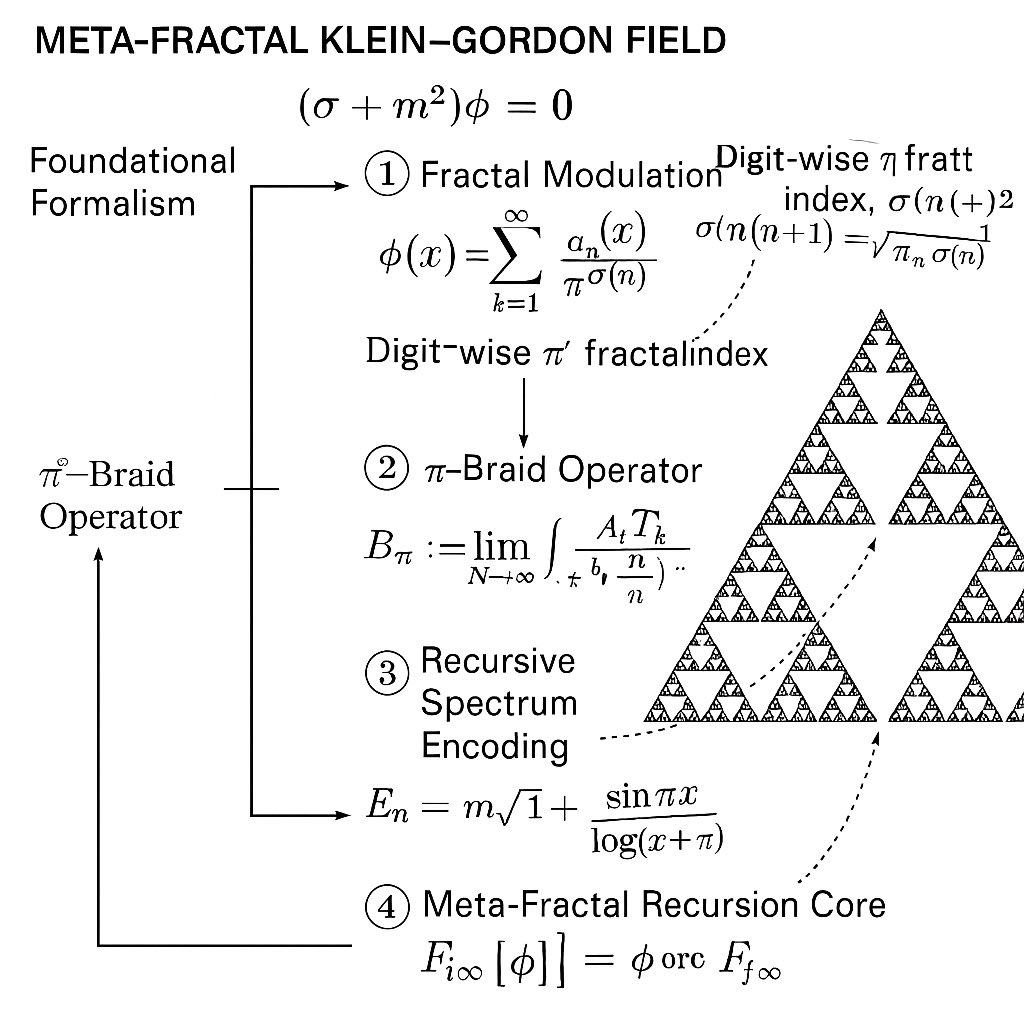
pure equation formalism for your Meta-Fractal Recursive Klein–Gordon Field indexed by non-repeating π digits and “impossible angles”:

⸻

🔷 X. Base Klein–Gordon Equation

(\Box + m^2)\,\phi(x) = X \qquad \text{with } \Box := \partial_t^2 - \nabla^2

⸻

🔷 X. Fractional-Time Generalization

\left[\,(-\partial_t^2)^{\alpha_n} + m^2\,\right] \phi_n(x) = X \qquad \text{for } \alpha_n := \frac{\pi_n}{10}

Where:
•\pi_n is the n^\text{th} digit of π
•\phi_n(x) is the nth recursive field

⸻

🔷 X. Recursive Superposition

\Phi(x) := \sum_{n=1}^{\infty} \phi_n(x)

Then:
\sum_{n=1}^{\infty} \left[\,(-\partial_t^2)^{\frac{\pi_n}{10}} + m^2\,\right] \phi_n(x) = X

⸻

🔷 X. Complex Angular Winding (Impossible Angles)

\phi_n(x, t) = e^{i\pi^n}\,\varphi_n(x, t)
\Rightarrow \left[\,e^{i\pi^n} (-\partial_t^2)^{\frac{\pi_n}{10}} + m^2\,\right] \varphi_n(x, t) = X

⸻

🔷 X. Meta-Fractal Operator Equation

Let \hat{\Pi} be the π-recursive operator:
\hat{\Pi} := \sum_{n=1}^{\infty} e^{i\pi^n} (-\partial_t^2)^{\frac{\pi_n}{10}}

Then the full equation becomes:
\left[\,\hat{\Pi} + m^2\,\right] \Phi(x, t) = X

![](https://pbs.twimg.com/media/GwLO1z3WgAA43eW.jpg)

XX engagements

![Engagements Line Chart](https://lunarcrush.com/gi/w:600/p:tweet::1946345435167154466/c:line.svg)

**Related Topics**
[digits](/topic/digits)
[chr](/topic/chr)

[Post Link](https://x.com/avalonaval/status/1946345435167154466)